En esta ocasión vamos a tratar unos circuitos particulares comúnmente conocidos como divisor, lo cierto es que se trata de un contador digital que tiene ciertas particularidades que le hacen reiniciarse desde cierta cuenta y esto lo hace de modo repetitivo. Pero vayamos por partes, en este tratado vamos a ver lo siguientes puntos:
El divisor digital elemental.
El divisor 74LS93 (TTL).
Divisor por 16
Divisor por 8 BCD
Divisor por 6
Divisor por 9
Divisor por 10
Divisor por 12
El divisor decimal 74LS90 (TTL).
Divisor por 10 en BCD
Divisor por 2, 4 y 5
Divisor por 2, 4, 8 y 9
INTRODUCCIÓN.
Cuantas veces a lo largo del día necesitamos llevar una cuenta de eventos, es un hecho que se produce de forma continua en infinidad de ocasiones, de manera tan simple que no reparamos en ello. Lo que realmente estamos haciendo cuando llevamos una cuenta, es cuantificar una serie de hechos repetitivos, estableciendo una cuenta de una serie de estos en un tiempo dado, el resto, muchas veces lo despreciamos.
Nos ocuparemos de los contadores digitales, uno de los requisitos más comunes en un equipo digital es el contador. Y el elemento contado, más común tiene que ver con el tiempo. Desde un reloj digital básico (incorporado en la mayoría de los equipos controlados digitalmente) a los cronómetros de intervalo y el contador de eventos, la necesidad de los circuitos contadores es muy grande.
Debido a esto, se requieren contadores para diferentes rangos de conteo y en todo tipo de circunstancias. Por ejemplo, un reloj digital simple, requiere de un contador decimal para las posiciones de unidades de segundos y minutos. Visto esto, vamos a estudiar una serie de circuitos integrados utilizados habitualmente como contadores, entre los que destacaremos la función de dividir como parte central. Un divisor, no es otra cosa que un contador al que se le aplica la condición de reiniciar su cuenta al llegar al final de la cuenta establecida por el usuario, como margen.
De hecho, los contadores son tan importantes en tantas y tan diferentes aplicaciones, que los tipos de CI’s contadores se han diseñado para familias de lógica TTL y CMOS. Algunos cuentan adelante para los relojes e intervalos de tiempo; otros cuentan abajo mostrando el tiempo que queda hasta algún evento. Algunos se diseñan específicamente para mostrar en modo decimal, mientras otros están en binario y aún otros, tienen un selector de rangos de cuenta. La lista de capacidades y opciones es bastante extensa, dejando mientras al diseñador del circuito con sólo la tarea de seleccionar el CI particular de las mejores prestaciones.
Una señal digital, está compuesta por una sucesión de impulsos llamados frecuencia que, proceden de un elemento que los genera o los procesa, en algunos casos, estos pulsos no siempre son uniformes, ni simétricos. La parte que, en estos momentos nos interesa de esta señal es muy concreta, tratamos de contar cuantos pulsos se producen en un tiempo establecido (intervalo), este tiempo si no se especifica lo contrario, es el segundo. Partiendo de esta condición, la cuenta que realizamos de una señal, se llama frecuencia. La frecuencia de una señal, se puede obtener teóricamente con la formula: 1Hz = 1/ segundo. El método alternativo para el cálculo es medir el tiempo entre dos repeticiones (período) y luego calcular la frecuencia (f) recíproca así:
F1
- Donde:
- T= (Período en segundos)
- f= (Frecuencia en Hertzios)
Contar en electrónica, como en otras disciplinas es un hecho muy común. Debido a que tenemos dispositivos que nos ayudan a realizar estas tareas, a continuación vamos a estudiar algunos circuitos integrados con los que podemos realizar tanto divisiones como cuentas.
El ciclo de servicio o rendimiento (duty cycle) de cualquier forma de onda rectangular se refiere al porcentaje del ciclo de la señal que permanece alto, en lógica 1. Si la señal pasa la mitad de su tiempo en lógica 1 y la otra mitad en lógica 0, tenemos una forma de onda con un ciclo de servicio o rendimiento del 50 %. Esto describe una onda perfecta, simétrica cuadrada.
Digamos que, dependiendo del ‘código’ establecido internamente por el fabricante del circuito integrado, podemos optar entre un contador binario o decimal, parámetro a tener muy en cuenta a la hora de utilizar cada tipo. Un contador digital básicamente es binario, y es cierto que, mediante una circuitería externa mas o menos sencilla, podemos convertir un contador binario, en contador decimal.
Hemos tratado diferentes contadores y distintos sistemas de uso, en estás páginas, entre dichos documentos podemos encontrar, distintas aplicaciones que utilizan estos dispositivos, sin embargo no hemos estudiado con detalle los contadores como tal. Aquí, veremos estos detalles y en algunos, sus diagramas de tiempo, para una mejor comprensión de lo descrito. Consideramos conveniente que se sigan los diagramas con detalle, es fundamental para su comprensión y posterior aplicación cuando sea necesario.
EL DIVISOR DIGITAL ELEMENTAL.
Vamos a describir aquí, cómo se comporta un divisor de frecuencias. Trataremos de frecuencias (en lugar de pulsos individuales que lleguen al azar a intervalos), si aplicamos un tren de pulsos de frecuencia fija a un contador comenzamos a notar algunas características interesantes y algunas relaciones útiles, entre la señal de entrada y la señal de salida.
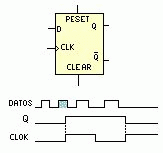
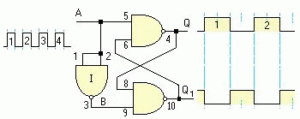Consideremos un flip-flop con una sucesión continua de pulsos de reloj y con una frecuencia fija, como el que se muestra a la derecha. Notamos tres hechos útiles sobre las señales de salida, vistas en Q y Q’:
- Las señales, están exactamente invertidas una de la otra.
- Las señales, son ondas cuadradas perfectas, rendimiento del 50 %.
- Las señales, tienen una frecuencia justamente la mitad del tren de impulsos de entrada.
El divisor digital, más simple es el compuesto por una báscula o flip-flop, elemento éste que puede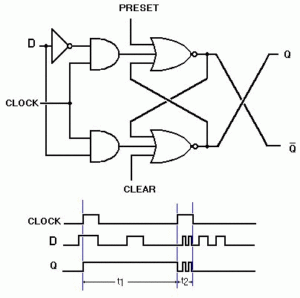 
estar formado por dos transistores y unos pocos componentes o por dos puertas lógicas conectadas en realimentación. En primer lugar, al tratar con flip-flops, alguien erróneamente, puede pensar que una frecuencia, sólo se puede dividir por números pares, la división de una frecuencia por un número impar también es posible, como veremos más adelante.
Este es, un ejemplo sencillo de un divisor de impulsos, puede observarse que de cada dos impulsos introducidos en A, en la salida Q, nos entrega la mitad, la puerta I es un inversor que se ha dispuesto en esa posición para evitar en lo posible los estados indeterminados que suelen aparecer en este tipo de básculas cableadas.
Otro ejemplo de un divisor sencillo es, la báscula D con puertas NOR que se muestra a la izquierda, sólo tiene una entrada de datos, debido a haber aplicado un inversor entre las entradas R y S, éstas, siempre estarán en oposición, lo que evitará la posibilidad de indeterminación, además se le ha dotado de una entrada de señal de reloj. Observamos que la salida Q = 1, cuando en la señal de reloj está a nivel lógico 1 y al mismo tiempo D = 1. Pasa a Q = 0 cuando haya caído D a 0 lógico y simultáneamente la señal de reloj pasa de nuevo a 1, es decir, la salida se presenta con el nivel alto de la señal de reloj, lo que se llama nivel activo de reloj.
El estado de salida se presenta únicamente en el instante en que la señal de reloj pasa de nivel lógico bajo a alto. Como vemos, la báscula D es una modificación de la báscula R-S, que mediante un inversor intercalado entre sus entradas R-S, elimina la posibilidad de indeterminación que presenta aquella.
El circuito de un flip-flop tipo D, es algo más que el circuito de una báscula tipo D, aunque parece muy similar, también tiene una única entrada de datos y una de reloj. Es bastante más complicado, la diferencia básica está en la nueva forma de utilizar la señal de reloj.
A veces, en los circuitos digitales, interesa asegurar que no pueda cambiar un dato de entrada durante el intervalo de ser transferido este dato a la salida entonces, se utiliza lo que se conoce como la técnica de ‘flanco de disparo’. Por consiguiente, llamaremos báscula a los elementos que utilicen el nivel activo de reloj y flip-flop a los que utilicen el flanco de subida o disparo.
Fig. 3
Un flip-flop tipo D, está constituido por dos básculas como entradas y una tercera báscula para la salida. Las básculas de entrada están interconectadas entre sí de forma que, al pasar la señal de reloj del nivel lógico bajo al nivel alto, se produce la entrada de estados complementarios de la báscula de salida.
A la derecha se muestra el símbolo del flip-flop J-K. El flip-flop J-K generalmente es el más utilizado, por ser el más versátil y sofisticado. Es similar a la báscula R-S, dispone de dos entradas de preselección éstas denominadas J-K, así como una entrada de reloj para su sincronización. La particularidad más genérica de los flip-flop J-K es que suelen estar controlados por el flanco descendente o de bajada de la señal de reloj, justo al contrario que lo hacen los flip-flop tipo D.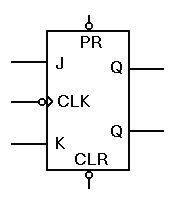
Nota. Las entradas negadas en los símbolos, generalmente se representan con un pequeño circulo junto al cuerpo del símbolo. En este caso, el dato se transferirá a la salida y se indica con el circulo por el flanco de bajada del CLK.
Para conectar los flip-flop J-K, disponemos de dos formas de configurar su activación:
- Disparo por flanco; el datos de la entrada se transfiere a la salida con la transmisión predeterminada de la señal de reloj.
- Disparo Maestreo-Esclavo; el dato de entrada se carga con el nivel alto de la señal de reloj y se transfiere a la salida con el flanco de bajada de la señal de reloj. En este caso, el dato de entrada no debe cambiar mientras la señal de reloj es alta.
El flip-flop J-K, actúa como se indica: si una de sus entradas tienen un nivel lógico 1 y la otra un nivel lógico 0, la salida Q se pondrá a 1 o a 0 con el flanco de bajada de la señal de reloj y permanecerá en este estado de salida, al igual que ocurre con la báscula R-S. Si ambas entradas están a nivel lógico 0, cuando lleguen los impulsos de reloj no cambiará, sin embargo si sus dos entradas están a nivel lógico 1, el flip-flop cambiará sus salidas con cada bajada del impulso de reloj; esto es lo que se llama trabajar en modo ‘balanceo’ (toggle en inglés). Este modo de trabajar es debido a que los niveles de las entradas J-K, se almacenan durante el tránsito del impulso de reloj, no cambiando durante ese tiempo su estado el biestable, una vez llega el siguiente flanco de bajada es cuando los datos almacenados hacen balancear el flip-flop.
Resumiendo, el funcionamiento del filp-flop J-K (maestro-esclavo), cuando J = K = 1, invierte el estado de las salidas Q y /Q con cada impulso de la señal de reloj. Este efecto, requiere de dos pasos de la señal de reloj para que el nivel de Q vuelva al estado inicial, esto realmente ha dividido la señal de reloj por dos. Todos estos son descritos con sobriedad en las lecciones de electrónica digital.
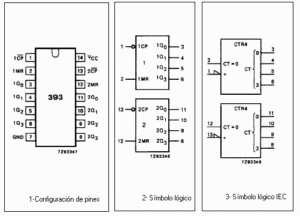
Un contador digital como es el circuito integrado 74LS393 es un divisor algo más complejo, se trata de un dispositivo constituido por un doble contador binario en su interior, cada uno formado por cuatro flip-flop Maestro-Esclavo, conectados de modo que nos permite realizar contadores de 4 bits (se pueden considerar dos 74LS93 en una cápsula) .
EL DIVISOR 74LS93 (TTL).
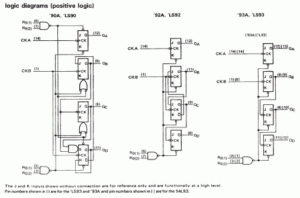
Como ejemplo entiendo que es suficiente lo anteriormente descrito, ahora vamos a abordar los circuitos integrados digitales comerciales, lo habitual en este caso sería hablar de los 74LS90 (decimal), 74LS92 (binario), 74LS93 (divisor de 4 bits), los patillajes DIL de los actuales y sus respectivas estructuras, se muestran a continuación.
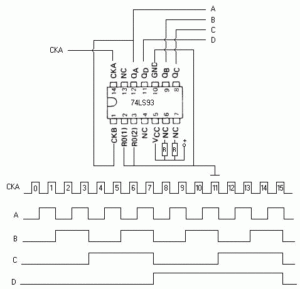
EL DIVISOR POR 16 EN BINARIO.
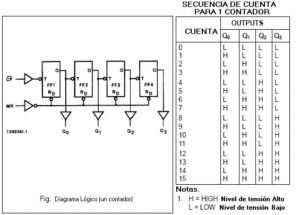
En la figura 04, puede apreciarse el modo de conexión interna entre sus patillas, atención a la tabla de verdad adjunta, tratando de comprender la secuencia de conteo seguida. El reloj CP es una señal negada y el reset maestro MR, permite poner a 0 la cadena de 4 filp-flop T, simultáneamente.
EL DIVISOR POR 8 EN BCD.
En la siguiente figura 06, presentamos el modo de configurar las entradas y salidas para conseguir un divisor por 8 y con salida codificada en BCD. Si comparamos esta figura con la anterior figura 05, podemos apreciar la aparente y sutil variación del resultado de conectar la salida QD (patilla 11) a las patillas 2 y 3 de puesta a cero, lo que hace que al llegar a 8 el contador dicha salida reponga a 0000, dando como resultado el reinicio del contador y por tanto del divisor.
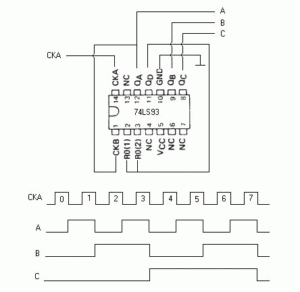
EL DIVISOR POR 6.
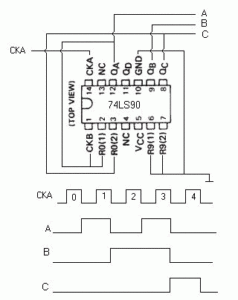
La forma de conectar el 74LS93, para obtener un divisor por 6 es muy sencilla, obsérvese el esquema de la figura 07 con su diagrama de tiempos y trate el lector de comprender su funcionamiento. Recordar que el primer FF es un divisor por 2 y la segunda entrada CKB corresponde a un segundo divisor por 8, formado por los 3 F-F restantes que conforman al 74LS93.
Fig. 9
Como ya se ha mencionado los impulsos aplicados a la entrada CKA, su salida QA por la (patilla 13), se aplica de nuevo a la entrada CKB (patilla 1) de la cadena de divisores siguientes, la salida QB se aplica a R01 y la salida QC a R02 y de este modo conseguimos nuestro objetivo. Esto esta muy bien, ya que estamos tratando de una serie de divisores en cadena y si pensamos un poco lograremos estos objetivos, no obstante parece menos viable conseguir un divisor por un número impar. La respuesta, la podemos ver a continuación.
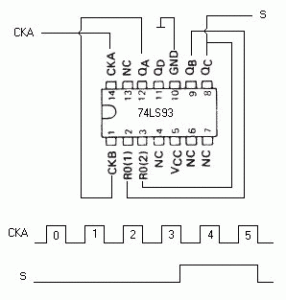
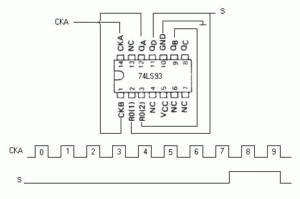
EL DIVISOR POR 9.
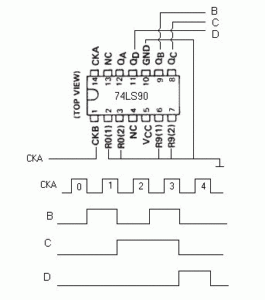
Con el fin de obtener la división por 9, hemos interconectado nuestro 74LS93 del modo que se aprecia en la figura 08. Como siempre, los impulsos se aplican a la entrada CKA y son recogidos en la salida S.
Fig. 10
La salida S es la unión entre la salida QD y la R02, como puede verse. Observar que el impulso de salida tiene un ancho de dos pulsos de entrada.
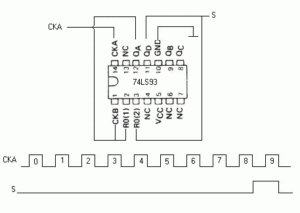
EL DIVISOR POR 10.
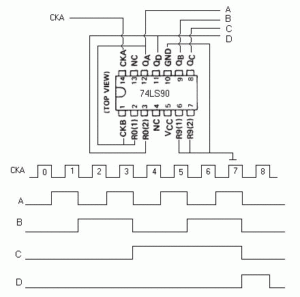
Para obtener un divisor por 10, el conexionado de las entradas y salidas del circuito integrado 74LS93 o similar, se debe corresponder con lo descrito en la figura 09 que se muestra debajo de estas líneas.
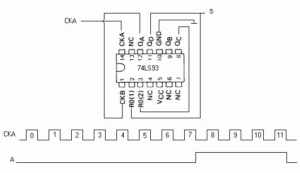
EL DIVISOR POR 12.
A fin de obtener un divisor por 12, muy utilizado (en su momento) en la generación de relojes electrónicos por su particularidad, podemos obtener si conectamos en un 74LS93 o similar, sus patillas según lo descrito en la figura 10.
EL DIVISOR DE DECIMAL 74LS90.
Por su versatilidad y utilidad en múltiples montajes que se han realizado desde siempre en la industria y en algunas aplicaciones descritas en estas páginas, describiremos la capacidad como divisor decimal, del circuito integrado 74LS90.
Fig. 13
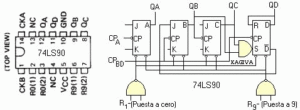
Este circuito integrado está compuesto por tres Flip-Flop Maestro-Esclavo y una báscula RS, dispone de dos entradas diferenciadas de reloj CPA para el primer Flip-Flop y CPBD, para B y D. Conectados de modo que nos proporcionan un divisor por dos y un divisor por cinco, separados, las entradas de conteo están inhibidas y las cuatro salidas puestas a cero lógico o a una cuenta binaria codificada a decimal (BCD) de nueve mediante líneas de reset directas con puertas. Como se puede apreciar en la imagen de la anterior figura 09, la salida QA no está conectada internamente a las siguientes etapas de conteo para una mayor independencia y versatilidad.
EL DIVISOR POR 10 EN BCD.
En la siguiente figura 12, mostramos la forma de obtener una división por 10 en código BCD mediante el circuito integrado 74LS90, este circuito está muy utilizado por la industria durante mucho tiempo y hacemos hincapié en que se comprenda el funcionamiento de este dispositivo ya que es la base para comprender los divisores digitales que se emplean en muchos de los procesos de la industria.
EL DIVISOR POR 2, 4 Y 5.
Para el divisor por 5 utilizando el 74LS90, disponemos de dos formas distintas para conseguir este tipo de divisor, en la figura 13, se muestra una de las dos formas posibles sin necesidad de ninguna puerta adicional.
Fig. 15
En la siguiente figura 14, presentamos la segunda forma de conseguir el divisor por 5, en esta ocasión se utiliza el segundo grupo de básculas o flip-flop disponibles en el dispositivo 74LS90.
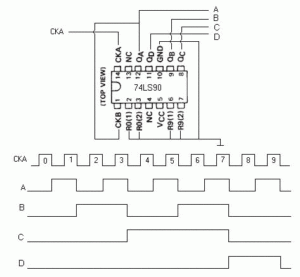
EL DIVISOR POR 2, 4, 8 Y 9.
En la figura 15, se muestra la forma de conectar el 74LS90 para conseguir que éste divida por 9.
Fig. 17
Habrá que observar que en cada divisor, dependiendo de la tecnología utilizada, el impulso del que se sirve un flip-flop para cambiar de estado, puede ser el flanco de subida o el flanco de bajada. Es decir, por ejemplo, viendo la gráfica de tiempos de la figura 15, se observa que el impulso CKA activa la salida A justo en su salida, o sea, al bajar su nivel lógico a cero, a esto se le llama flanco de bajada, lo que nos indica que la salida A se activa en su flanco de subida y no cambia su estado lógico hasta que, se produce un nuevo flanco de bajada en el impulso de CKA, en este caso se produce el cambio de estado de la salida A que, vuelve a cero. También se les suele llamar flanco izquierdo y flanco derecho respectivamente, en algunos tratados.
ACLARACIÓN.
La importancia y utilidad de los divisores en sus variantes, radica en la precisión, por ejemplo, en la necesidad de conocer la frecuencia exacta de una señal electromagnética del tipo que sea, ya que cuanto mayor sea la exactitud de la división tanto mayor será la precisión de la medición realizada con dicha división.
Otro ejemplo podríamos hallarlo en la medición del tiempo, un hecho tan natural como es conocer la hora y sin embargo, este hecho hace necesario realizar un oscilador de muy alta frecuencia y que cuya frecuencia sea estable, que no varíe, influenciada por la temperatura o los parásitos electromagnéticos del entorno o por las variaciones de la tensión de alimentación, entre otros.
Esa frecuencia ideal, tendría que reducirse de algún modo, esto es, dividirla en una porción exacta que, siempre y en cualquier momento nos de invariablemente en la salida, la misma cuenta, de este divisor depende directamente la exactitud de nuestro reloj, por ese mismo motivo se necesita una frecuencia muy alta, precisamente para poder hacer una división lo más pequeña posible como puede ser una fracción de segundo, para utilizarla posteriormente en la cuenta del tiempo. Pero bueno, eso se trata con más profundidad en los tratados especializados en la medición del tiempo y frecuencímetros que, están fuera de este tratado.
Por el presente consideramos que ha quedado descrito con bastantes ejemplos los diferentes tipos de divisores lógicos y las capacidades de los dispositivos que nos presenta la familia TTL. En un próximo caso abordaremos si se considera necesario el uso de la familia CMOS.